Pinned
The Dinamics of a Space Torus
To construct a solid-state device that produces power based on the geometry, we need to understand the principles and laws of motion so well that we can replace the mechanical motion with the motion of the fields themselves to generate EMF. For this, we need to understand the dynamics inside a Space Torus perfectly, because this Torus replicates every time we havea moving body or signal. This succession or replication we call it Space Tori (Plural). In tommorow meeting, we will talk about Centrifugal Force, Momentum, and how acceleration and pressure can lead to higher potential, and how these ideas relate to the prototypes. Have a look at the text and images, so you can be more familiar with the terminology and have a better visual understanding of these ideas. Everything in life is in constant motion, and if we truly understand the dynamics of the space torus, we can unlock unlimited potential in many different ways. A Space Torus is formed by the interaction of Kinetic and Potential energy flows as a response, while any motion is present through space. Generally, there are 3 components: 1. Meridian Plate Circuits (Axial Loops) 2. Concentric Orbits (Equatorial/Tangential Loops) 3. The Central (Primary) Axis (Axis X) Meridian Plate Circuits (Axial Loops) • Definition: In contrast to the equatorial orbits, the loops that travel through the center and around the outside ( pole-to-pole) are called meridian plate circuits. • Shape: While technically spheres, these loops are so deformed by field pressures that they appear as flattened, polarized plates. • Function: In a magnet, millions of these meridian plates are packed together to form the characteristic "apple-shaped" field,. Relationship and Interaction • Focal Points: Because the axial meridian loops are bundled in orderly concentricity, their collective center points form the concentric orbits found on the equatorial plane. • Particle Creation: Discrete quanta of energy, such as electrons, are created at the centers of these circuits.

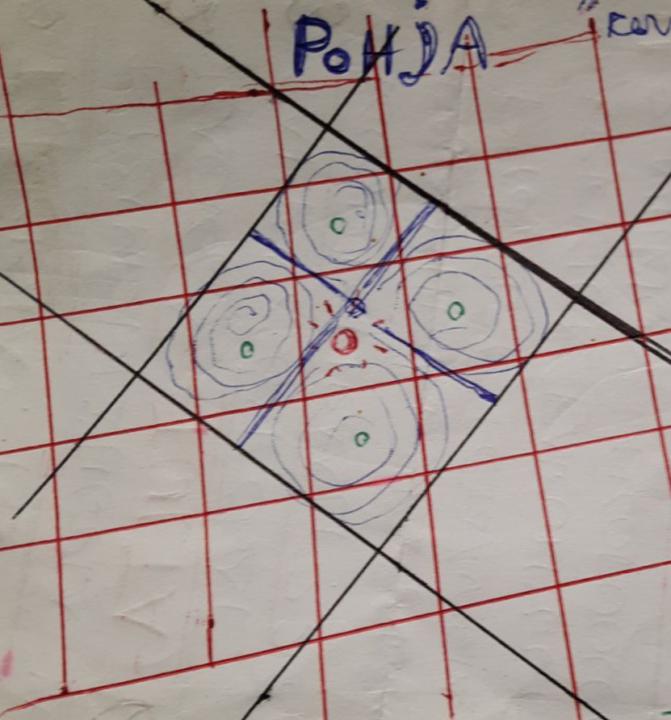
Energy-grid Layout
This is a very crudely done layout picture of the "checkerboard" energy-grid, but it will help to get the point. My father has been mapping them independently for over 20 years, along with trees and plant fields, crystals fields and all the conscious fields along that. Better sketches are coming later. The Black lines are downward going energy "walls", they have a big force in them, it feels bad to stand on them for a long period. Each side of the line is ~6m long. The corners point to cardinal points, north-south-west-east. We call them *Earth penetrating lines*. The Red lines are smaller and upward going energy walls they "overlap" the Earth penetrating lines. We call them *Ascending lines*. Each side of the line is 2m long. Also being on these lines for long period can make you restless, not as much as on the penetrating lines tho. Its corners point to half-cardinal points. At each of the energy-grid "arks" there is at the most middle point an beam or pillar of energy we call the *Middlepole*. (Its marked as red dot on the picture.) It shoots up to the northern sky, somewhere up to the "Polaris star". This middlepole feels very sacred and powerful. Same kind of energy pole is also on top of any fire. It can be felt by just watching the fire without any thoughts in mind. Then breathing inside and allowing eyes to travel upwards over the flame/candle. Very uplifting. Then about meter to north from the Middlepole is a *Spring* which "bubbles" almost water-like energy from underground. (Its marked as the blue dot on the picture.) At different times the Spring might shoot the "waters" with high pressure. Forth from it flows 4 small *Streams/Channels* which stop at the *Earth Penetrating walls* and goes down with them, thus dissecting the Ark into 4 sections. Now in each of these 4 sections there are the *Vortexes*. My english is not well enough to portray how the vortexes look like. (They are marked on the picture as the green dots and swirls.) In each section the vortexes are mirroring the opposite vortex.
A Biorhythm Tool Inspired by the Ra Material
Here is the compiled Ra material on biorhythms and the 18-day cycle, drawn from the relevant sessions. Read carefully. See the link to the simple calculation tool provided by L/L Research and my own Claude Artifact that does the same thing and you can modify if you wish. ----- **The Four Cycles** (61.3) Ra states there are four types of cycles given at the moment of entry into incarnation. Three are known among humans as biorhythms. The fourth Ra calls “the cycle of gateway of magic of the adept or of the spirit,” completed in approximately eighteen diurnal cycles. The cosmic patterns are also a function of the moment of incarnative entrance and have to do with the moon, the planets of the galaxy, the galactic sun, and in some cases instreamings from major galactic points of energy flow. ----- **The 18-Day Adept Cycle — Structure** (64.10) The spiritual or adept’s cycle is an eighteen-day cycle operating with the qualities of the sine wave. The first nine days constitute the positive side of the curve. Within those nine days, precisely the fourth, fifth, and sixth days are when workings are most appropriately undertaken, given that the entity is still without total conscious control of its mind/body/spirit distortion/reality. The critical points are the transitions: passing from the ninth to the tenth day, and from the eighteenth to the first day. The adept will experience difficulty at these points, especially when a transition is occurring in another cycle simultaneously. At the nadir (the lowest point of the cycle), the adept is at its least powerful but is not open to difficulties in nearly the degree experienced at the critical transition points. ----- **Calculating the Cycle** (64.11) Ra confirms the cycle begins at the instant of birth — specifically, the diurnal cycle upon which the birthing event occurs is satisfactory for all but the most fine workings. The precise instant is not necessary to identify. ----- **Efficacy and Balance** (64.12, 64.13)
0
0
Intro to The Alchemical Manual For This Millennium (generated podcast format)
UPDATED (full upload, please read carefully): Please find the introduction* and all 12 chapters in "podcast" format below. The suggested way to use this is to listen to the chapters in your time, then go over the corresponding book section carefully. Especially the visuals. Expect possible errors and misinterpretations in the audio format. This is not an audio book, but an attempt to make extremely dense material more accessible. Remember the authors' advice: don't get stuck when something appears incomprehensible, go through and expect to repeat the journey multiple times. Original description: This book continues to intrigue** me. Its breadth, scope and density are unmatched. Strongly suggest you pair it with the Ummo Disclosure, Edward Leedskalnin and Itzak Bentov's books. The consistency is encouraging. I took the freedom to run it through NotebookLM and turn a small overview of it in the form of a synthetic podcast. Sharing here for others like me who probably hadn't heard of this before and might still be on the edge before investing the time to look into it in depth. Best wishes, I hope to meet many of you tomorrow! *The original overview file was replaced with one that introduces the chapters and the following 12 episodes. **I thought hard about who wrote this book. The spirit, ethics and philosophy behind it make me think this is written by Lemurian souls. Similar to the Ra Material, there is a sense of past mistakes in communication that this material seems to be atonement for. The commentary about predation and the food chain is particularly relevant. I strongly invite you to reflect on the source of any material we use.
Tachion and Etheric Energy, Quartz Crystals, Amber as Transducers
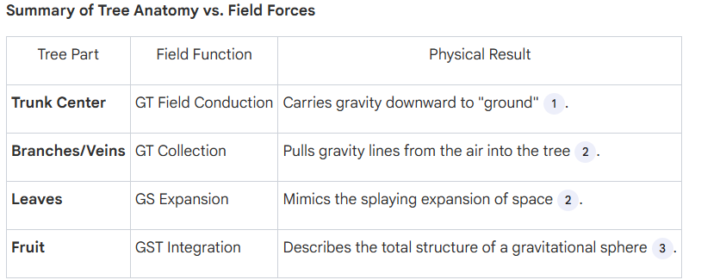
In the attached 1st Audio recording, Bashar talks in the same way about Etheric and Tachion Energy, and he mentioned the Amber and quartz Crystals as transmitters or transducers of that energy. Mainstream Definition: Tachyon energy — hypothetical faster-than-light particles (tachyons) proposed in some fringe theories. Claimed to carry "pure energy" that can heal, raise vibration, or transmit information instantly. This faster speed is in alignment with the idea of higher octaves mentioned in the Alchemical Manual, where we have higher speeds because the density of the higher dimensions is much lower and has less impedance. Also in the document, they talk about trees as perfect prototypes of Space-Time Antennas. Here is a Summary: Trees are considered the most important prototypes for earthly field separation and integration because they physically demonstrate the dynamic interaction between the Space (S) and Time (T) fields. Every part of a tree—from its roots to its fruit—mirrors the geometry and movement of the Gravitational Space-Time (GST) Fields,. Here is how the anatomy of a tree functions as a living model of Symmetric Field Physics: The Dual Directional Flow A tree utilizes the directional flows of gravity to grow and sustain itself: • The GS Field "Ladder": The tree grows upward by climbing the Gravitational Space (GS) Field like a ladder. The expanding nature of this field allows the tree to fill available space as it divides and branches. • The GT Field "Grounding": Simultaneously, the center of the trunk "walks" the Gravitational Time (GT) Field downward to be grounded in the Earth. • Spiral Interaction: As long as the GT Field flows downward through the trunk, the GS Field spirals upward around it, creating a balancing sheath of energy. Geometric Mimicry of Fields Trees do not just inhabit fields; their physical structures are designed to mimic the patterns of those fields: • Leaves: Each leaf mimics the pattern of GS Field expansion. • Veins and Branches: Each branching limb and leaf vein acts to gather more GT Field lines, funneling them into the trunk to be carried toward the ground.
1-30 of 70
powered by

skool.com/allistar-center-4289
This is the Metafusion community blending Technology with Consciousness, Science with Metaphysics. We connect what seems to be polarity into one idea.
Suggested communities
Powered by



